An abstract concept
When I first started with electrochemistry, I found the notion of interface potentials rather daunting and abstract. Since then, I have seen new students and seasoned professionals alike struggling to differentiate between the various types of electrochemical potentials. In particular, some people erroneously use the term “REDOX potential” as a general term to refer to entirely different concepts. This article discusses the differences between the two primary interface potentials: the reversible and the open circuit or corrosion potentials.
The simplest electrochemical cell
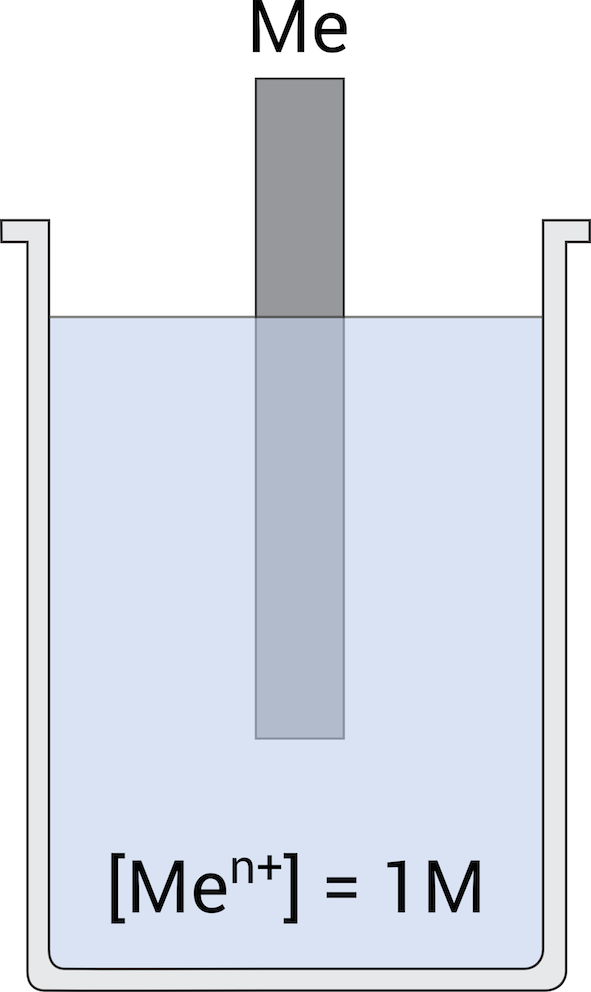
When I ask new corrosion students “what is the simplest electrochemical cell you can construct?” the answer is often some form of metal rusting in some electrolyte. However, as we will see below, the case of a metal, such as iron, exposed to an electrolyte, such as seawater, is a very complex electrochemical system. The simplest electrochemical cell consists of a metal (Me) exposed to a solution of its cations (Men+), Figure 1. Even in this simple case, we need to determine what it is happening at the surface of the electrode.
Thermodynamic equilibrium – a dynamic condition
A metal, Me, immersed in an electrolyte containing a finite amount of its metal cations, Men+, will reach thermodynamic equilibrium after a certain exposure time (Note: what happens at the Me/solution interface upon exposure will be the topic of a separate post). At equilibrium, dissolution and reduction (i.e. plating out of Men+) take place at the same rate, Equation 1.
$$M{e^{n + }} + n{e^ – } \leftrightarrow Me \tag{1}$$
However, since this is a reversible reaction, there is no net mass change. Thermodynamic equilibrium is, thus, better viewed as a dynamic condition.
Under standard state conditions, i.e. temperature = 25°C, gas fugacity = 1 atm, and activity of solid and liquids equal to 1 M, the half-cell reduction reaction Men+/Me is at the standard reversible potential, E0. The term reversible suggests that oxidation and reduction reactions occur at the same rate. E0 is also referred to as REDOX potential in some electrochemistry books.
A listing of half-cell electrode potentials constitutes the electromotive force (EMF) series. Since the EMF series lists standard potentials describing thermodynamic equilibrium in which the reaction goes back and forth at the same rate, there is only one potential for both oxidation and reduction. The difference in polarity is simply one of convention. In the EMF series, all reactions are written as reduction reactions. This sign convention was established by the Stockholm Convention of 1953, which chose reduction as the common direction of electrochemical reactions. Oxidation potentials are identical in magnitude but have opposite sign.
Reversible potentials in conditions other than the standard state
For a generic electrochemical reaction of the form:
$${\text{Oxidized}} + n{e^ – } \rightleftharpoons {\text{Reduced}}$$
The reversible potential, ERev, in conditions other than the standard state is calculated using the Nernst equation (LaTex code). The Nernst equation describes a relationship between the standard reversible potential, the activity of the oxidized and reduced species involved in the electrochemical reaction, and temperature, Equation 2:
$${{\text{E}}^{\text{Rev}}} = {{\text{E}}^{\text{0}}} – \left( {\frac{{R \cdot T}}{{n \cdot F}}} \right) \cdot \ln \left( {\frac{{\prod {{{\left( {{a_{{\text{Red}}}}} \right)}^j}} }}{{\prod {{{\left({{a_{Ox}}} \right)}^k}} }}} \right) \tag{2}$$
Where:
| Term | Definition | Value | Units |
|---|---|---|---|
| \(E^{Rev}\) | Reversible Potential | – | V vs. Reference} |
| \(E^{0}\) | Standard Potential | – | V vs. Reference} |
| \(R\) | Universal Gas constant | 8.3144621(75) | \(\frac{J}{{^\circ C \cdot mol}}\) |
| \(T\) | Temperature | – | \(^\circ C\) |
| \(F\) | Faraday’s constant | 96,485.3399(24) | \(\frac{C}{eq}\) |
| \(n\) | Number electrons | – | \(\frac{eq}{mol}\) |
| \(a_{Red}\) | Activity reduced species | – | – |
| \(a_{Ox}\) | Activity oxidized species | – | – |
| \(j\) and \(k\) | Stoichiometric coefficients | – | – |
A mixed potential – multiple electrochemical reactions
Although important when studying electrochemical reactions, a metal in a solution of its own ions is of little relevance to corrosion. In this regard, a corroding system is far from thermodynamic equilibrium. To draw a parallel with the previous example, the simplest corrosion experiment consists in immersing a reactive metal, e.g. zinc (Zn), in a deaerated strong acid, e.g. HCl, Figure 2.
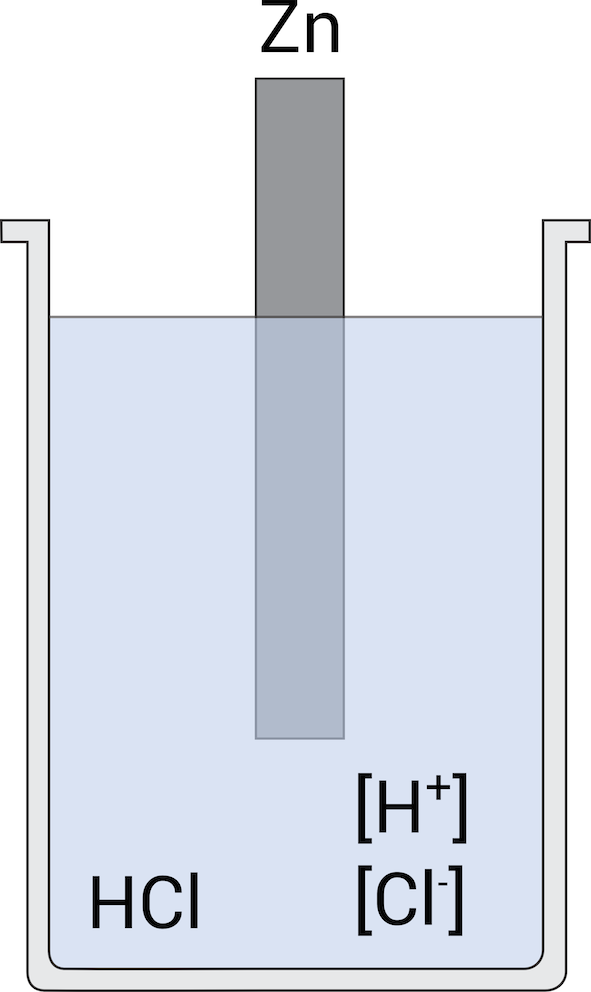
In this case, two different electrochemical reactions occur simultaneously at the surface. The anodic reaction is the oxidation of the metal, Equation 3, whereas the cathodic reaction is the reduction of protons, H+, to hydrogen gas (H2), Equation 4.
$$ {Zn} \to {Zn^ {2+} } + 2{e^ – } \tag{3}$$
$$ 2{H^ + } + 2{e^-} \to {H_2}(g) \tag{4}$$
The example describing a piece of iron immersed in seawater is a much more complex problem. In its simplest form, the anodic reaction is the oxidation of iron to ferrous ions, Fe2+, Equation 5. There are, however, two possible reduction reactions depending on solution pH, dissolved oxygen concentration, and the hydrodynamics of the electrolyte. The two possible cathodic reactions are the oxygen reduction reaction (ORR), Equation 6 or 7, and the reduction of H+/H2, Equation 4, or the direct reduction of water to H2, Equation 8. We say that there are two, rather than four, possible cathodic reactions in this example because Equations 6 and 7 and Equations 4 and 8 are equivalent.
$${Fe^ {2+} } + 2{e^ – } \to {Fe} \tag{5}$$
(neutral – basic pH) $${O_2}(sol.) + 2{H_2}O + 4{e^ – } \leftrightarrow 4O{H^ – } \tag{7}$$
(neutral – basic pH) $$2{H_2}O + 2{e^ – } \leftrightarrow {H_2}(g) + 2O{H^ – } \tag{8}$$
The principle of charge conservation dictates that the sum of all oxidation currents must equal the sum of all reduction currents to avoid the accumulation of charge on a freely-immersed electrode, Equation 9:
$$\sum\limits_{}^{} {{I_{{\text{Ox}}}} + \sum\limits_{}^{} {{I_{{\text{Red}}}}} } = 0 \tag{9}$$
An electrode immersed in an electrolyte will naturally develop an interface potential. This interface potential is referred to as corrosion potential, Ecorr, or open circuit potential, EOC. Ecorr is the potential at which the sum of anodic currents equals the sum of cathodic currents, Equation 10. The current at EOC is the corrosion current Icorr.
$${I_{{\text{Ox}}}} = {I_{{\text{Red}}}} \equiv {I_{{\text{corr}}}} \tag{10}$$
It is important to realize that the electrode is not at thermodynamic equilibrium at EOC: the metal is being oxidized and water or other oxidants are being reduced. The corrosion potential is, therefore, a mixed potential as predominant anodic and cathodic reactions are different.
A listing of corrosion potentials in a given electrolyte constitutes a galvanic series. A galvanic series shall not be confused with the EMF series, which lists reversible reduction potentials.
Summary
- The reversible potential represents thermodynamic equilibrium.
- At thermodynamic equilibrium there is no net mass loss: dissolution rate equals reduction rate.
- Most systems undergoing corrosion are far from thermodynamic equilibrium.
- There are multiple anodic and cathodic reactions occurring simultaneously at the surface of an electrode that is away from thermodynamic equilibrium.
- The corrosion potential is the potential at which anodic and cathodic reaction rates are equal.
Recommended reading
If you like to learn more about interface potentials and thermodynamics, I strongly suggest you check the following sources:
- R. W. Revie, H. H. Uhlig, “Corrosion and corrosion control: an introduction to corrosion science and engineering” (2008): p.31. Buy the book at Amazon or Kindle Edition.
- P. R. Roberge, “Corrosion Engineering: Principles and Practice,” McGraw-Hill Professional (2008). Buy the book at Amazon or Kindle Edition.
- D. A. Jones, “Principles and Prevention of Corrosion,” Prentice Hall, 2 ed.(1995): p.44. Buy the book at Amazon.