About Corrosion

All about corrosion science and engineering

Is there a right way to plot polarization curves?

by

Historically, polarization curves were determined galvanostatically, i.e. by applying a constant current and measuring the resulting electrode potential \( E \). The reason for this was a simple one. Before the advent of solid state electronics, galvanostats were simpler to construct and operate than modern potentiostats, which rely on complex electrometer circuitry.

As a result, polarization curves were traditionally plotted as \( E \) vs. current density \( (i) \), or alternatively \( \log i \).  In other words, \( i \) was taken as the independent variable. Standards such as ASTM G3, ASTM G5, and ASTM G61 recommend this approach, which still is the most popular in the U.S.1–3  Figure 1 shows an anodic cyclic potentiodynamic polarization curve of UNS N08020 in 3.5 wt% NaCl pH 8.0 at 25 ℃ plotted in accord with ASTM G61.

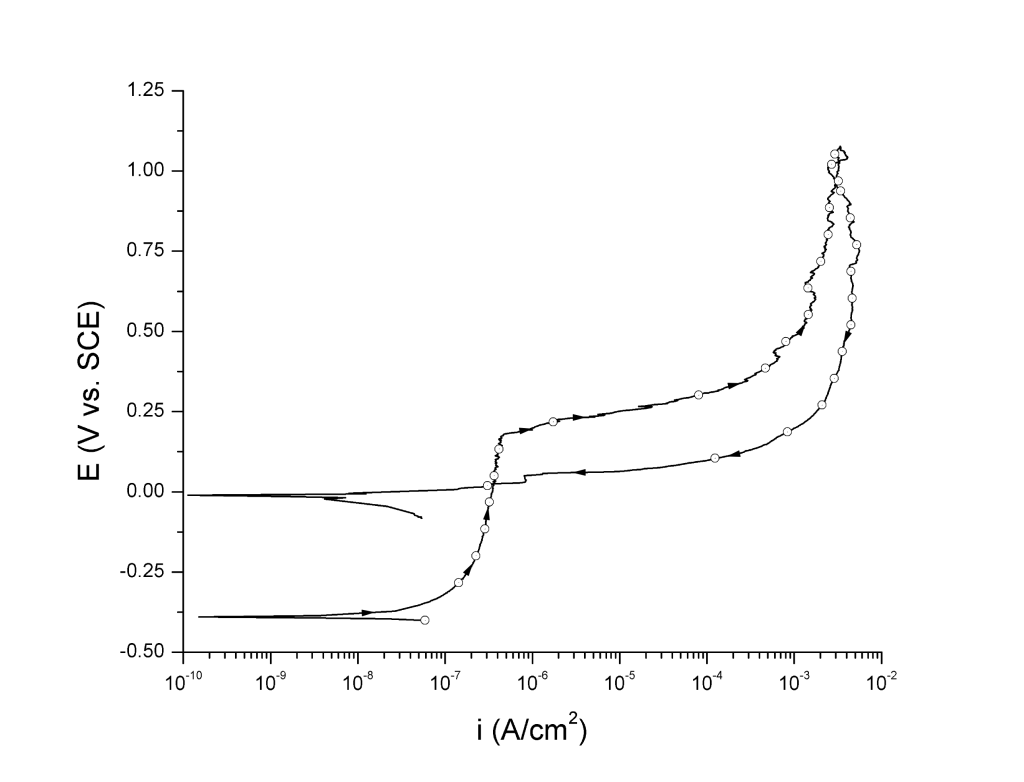
UNS N08020 anodic potentiodynamic polarization curve in 3.5 wt% NaCl pH 8.0 at 25 ℃ plotted according to ASTM G61 standard.
Figure 1. UNS N08020 anodic potentiodynamic polarization curve in 3.5 wt% NaCl pH 8.0 at 25 ℃ plotted according to ASTM G61 standard. Arrows indicate the direction of the potential scan.

Today, however, polarization curves are determined either potentiostatically or potentiodynamically. Independently of whether the test is static or dynamic, in a conventional 3-electrode setup the potentiostat controls the voltage difference between a Working Electrode (WE) and a Reference Electrode (Ref) by injecting a current through a Counter Electrode (CE). In Europe and South America, for example, \(i\) vs. \( E \) (or  \( \log i \) vs. \( E \)) plots are the norm. Figure 2 shows the same polarization curve but taking \(E\) as the independent variable.

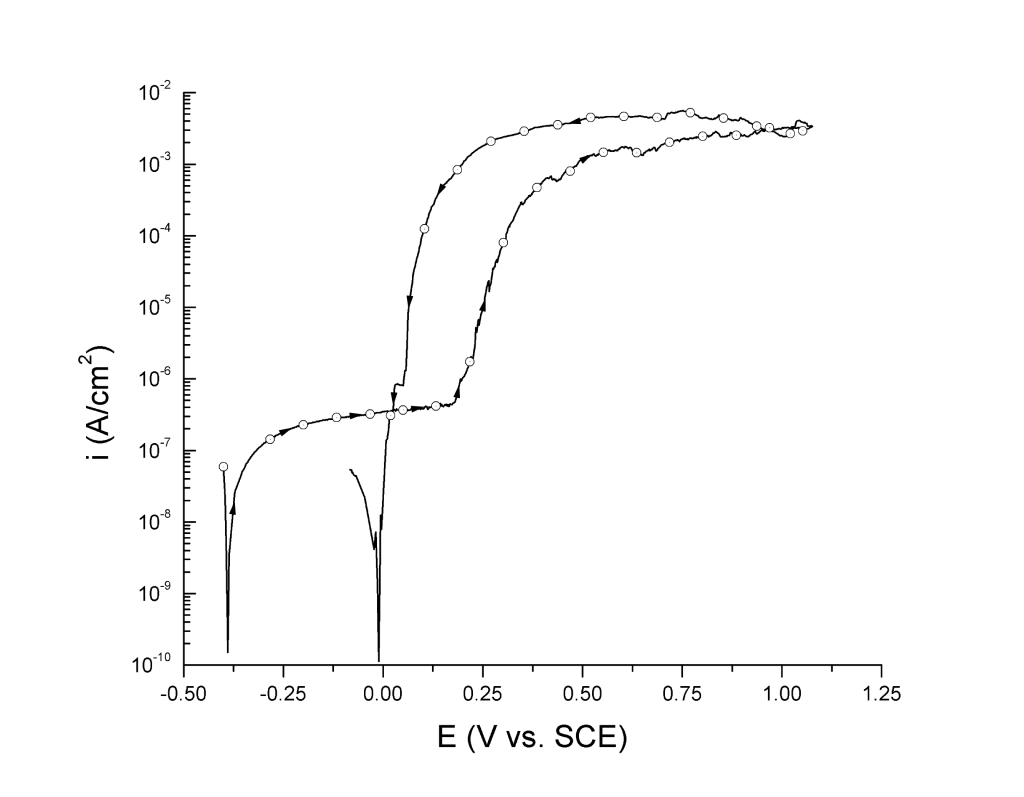
UNS N08020 anodic potentiodynamic polarization curve in 3.5 wt% NaCl pH 8.0 at 25 ℃ plotted as E (independent variable) vs. i.
Figure 2. UNS N08020 anodic potentiodynamic polarization curve in 3.5 wt% NaCl pH 8.0 at 25 ℃ plotted as E (independent variable) vs. i. Arrows indicate the direction of the potential scan.

Which way is the correct way?

A question that bears asking is whether there is a right way to plot polarization curves. In this regard, McCafferty strongly argues that, based on absolute reaction rate theory, the electrode potential is the true independent variable and shall be plotted on the abscissa in a polarization curve.4

I personally think that any professional shall be able to read polarization curves independently of how they were plotted. I prefer \( E \) vs. \( i \) curves, but that is just me. In this blog, I will mix \( E \) vs. \( i \) and \( i \) vs \( E \) curves so the readers becomes familiar with both approaches. Regardless of how we represent the \( E-i \) space, it is important to remember that polarization curves can give invaluable information about anodic and cathodic reaction mechanisms and are, thus, one of the most important tools for the corrosion scientist and engineer.

Reading Tafel constants

Finally, I like to make an observation about Tafel constants. For activation polarization, anodic and cathodic Tafel constants or slopes (\( \beta _a \) and \( \beta _c [latex], respectively) are a measure of the overpotential needed to increase the resulting current density by one decade. Independently of how polarization curves were plotted, Tafel slopes are conventionally expressed in terms of volts per decade [latex] (\frac{V}{{dec}}) \). It is imperative, therefore, to pay attention to the way the \(\) E-i \(\) space was drawn to be consistent with this definition. We will cover activation polarization and revisit Tafel’s and Stern and Geary’s original work on a later post.5

References

  1. ASTM G3, 2013, “Standard Practice for Conventions Applicable to Electrochemical Measurements in Corrosion Testing”, ASTM International, West Conshohocken, PA, 2003, DOI: 10.1520/G0003, www.astm.org.
  2. ASTM G5, 2013, “Standard Reference Test Method for Making Potentiodynamic Anodic Polarization Measurements”, ASTM International, West Conshohocken, PA, 2003, DOI: 110.1520/G0005, www.astm.org.
  3. ASTM G61, 2009, “Standard Test Method for Conducting Cyclic Potentiodynamic Polarization Measurements for Localized Corrosion Susceptibility of Iron-, Nickel-, or Cobalt-Based Alloys”, ASTM International, West Conshohocken, PA, 2003, DOI: 10.1520/G0061–86R09, www.astm.org.
  4. E. McCafferty, “Introduction to corrosion science” (Springer, New York, DOI 10.1007/978–1–4419–0455–3, 2009):p.136. Buy at Amazon.com.
  5. M. Stern and A. L. Geary, “Electrochemical Polarization: I . A Theoretical Analysis of the Shape of Polarization Curves“,  J. Electrochem. Soc. 104 (1957): p.56-63; doi:10.1149/1.2428496.

Acknowledgments

Many thanks to Dr. Mauricio Rincón-Ortiz for providing the polarization curves!